חישוב שטח משולש

את שטח המשולש ניתן לחשב לפי הנוסחה הידועה של חצי מכפלת גובה המשולש באורך הצלע שאליה הגובה יורד,

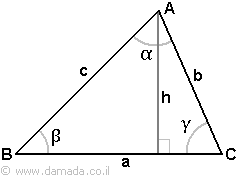
משולש חד-זווית

S = ½ a•h

אם אורכו של הגובה לא ידוע, אז נצטרך לבטא אותו בעזרת גדלים אחרים במשולש כמו הזוויות או צלעות אחרות.

נבדוק כיצד ניתן להחליף את ערכו של הגובה בביטוי אחר עבור שלושת סוגי המשולשים.

חישוב שטח משולש חד-זווית

ניעזר במעט טריגונומטריה ונקבל,

sin γ = h/b
h = b sin γ

S = ½ ab•sin γ

נוכל להשתמש בזווית אחרת ולקבל,

sin β = h/c
h = c sin β

S = ½ ac•sin β

בשני המקרים קיבלנו ששטח המשולש שווה לחצי המכפלה של סינוס זווית במשולש בשתי הצלעות הסמוכות לה.

בעזרת הורדת גובה אחר במשולש ניתן להוכיח את תקפות המשפט שלעיל גם עבור הזווית α.

חישוב שטח משולש ישר-זווית

נשים לב שעבור משולש ישר-זווית נקבל שהנוסחה מצטמצמת בהצבה של הזווית הישרה בה,

שרטוט

משולש ישר-זווית

S = ½ ab•sin 90º
S = ½ ab

וזוהי הרי הנוסחה הידוע לחישוב שטחו של משולש ישר-זווית, שהוא מחצית שטח המלבן המתקבל מהכפלת שני הניצבים של המשולש זה בזה.

הנוסחה לחישוב שטח המשולש שנמצא עבור זווית חדה במשולש חד-זווית מתקיימת גם עבור זווית ישרה במשולש ישר-זווית.

הנוסחה גם מתקיימת עבור זווית חדה כלשהי במשולש ישר-זווית. הוכיחו זאת!

חישוב שטח משולש קהה-זווית

במשולש קהה-זווית נחשב את שטח המשולש פעם לפי הזווית הקהה, α, ופעם לפי הזווית החדה, β.

שרטוט

משולש קהה-זווית

sin(180º- α) = h/b
sin α = h/b
h = b sin α

S = ½ hc = ½ bc sin α

כעת נחשב לפי הזווית β (יכולנו באותה מידה לבחור כדוגמה לזווית חדה את הזווית γ, אך עם סימון אנך אחר). נקבל,

sin β = h/a
h = a sin β
S = ½ hc = ½ ac sin β

כלומר אותה נוסחה לחישוב שטח המשולש שנמצאה עבור זווית חדה במשולש חד-זווית ועבור זווית ישרה במשולש ישר-זווית מתקיימת גם עבור זווית קהה ועבור זווית חדה במשולש קהה-זווית.

[לפרק הקודם | לפרק הבא]

[ חזרה לראש העמוד ]

[ עמוד הבית | אודות | זכויות יוצרים | מפת האתר ]