המצולע
בעזרת הישרים ניתן לשרטט צורות שונות. ראשית נבחין בין צורה פתוחה ובין צורה סגורה. צורה פתוחה היא צורה שאין לה שטח פנימי כלוא. צורה פתוחה היא חופשית למעבר מכל צדדיה. צורה סגורה מאופיינת בכך שהיא סוגרת, תוחמת וכולאת שטח פנימי בתוכה. אל תוך השטח הפנימי הכלוא בצורה סגורה לא ניתן להיכנס מבלי לחצות את אחד הישרים של הצורה.

דוגמאות לשני סוגי צורות
נשים לב שלא ניתן ליצור צורה סגורה בפחות משלושה קטעים ישרים.
מצולע הוא צורה סגורה המורכבת משלושה קטעים ישרים או יותר. כל קטע ישר השייך לצורת המצולע נקרא צלע (מכאן שמו של המצולע). כל נקודת מפגש בין שתי צלעות במצולע נקראת קודקוד. בנקודת מפגש זו מוגדר גודל הזווית שבין שתי הצלעות. קודקוד הזווית שבין שתי הצלעות מתלכד עם קודקוד המצולע.
מספר הקודקודים במצולע, מספר הזוויות הפנימיות במצולע ומספר הצלעות במצולע הם כולם שווים!
כעת נבחין בין צורה סגורה קמורה ובין צורה סגורה שאינה קמורה. צורה סגורה קמורה היא צורה סגורה בה אף צלע או המשכה אינם חותכים את המצולע . בצורה סגורה שאינה קמורה ישנה לפחות צלע אחת שהיא עצמה או המשכה חותכים את המצולע.
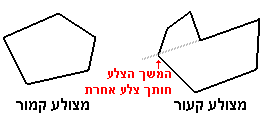
דוגמאות לשני סוגי מצולעים
במדריך זה נדון, כפי שנראה בהמשך, רק בצורות סגורות קמורות.
דוגמאות למצולעים סגורים וקמורים הם, למשל,
המשולש – בעל שלוש צלעות המרובע – בעל ארבע צלעות
המחומש – בעל חמש צלעות
המשושה – בעל שש צלעות
המתומן – בעל שמונה צלעות

דוגמאות לסוגי מצולעים שונים
סכום סך הזוויות הפנימיות במצולע קמור נתון על-ידי הנוסחה,
כאשר n הוא מספר הצלעות במצולע.
הקף המצולע הוא סך אורכי כל צלעותיו.
שטח המצולע הוא השטח הכלוא על-ידי צורת המצולע.
מצולע משוכלל הוא מצולע בו כל הצלעות שוות באורכיהן. במצולע משוכלל גם כל הזוויות (הפנימיות) שוות בגודלן. גודל כל זווית (ומעתה נדון רק בזוויות פנימיות, אלא אם מצוין אחרת) במצולע משוכלל הוא 180º • (n-2)/n.

דוגמאות למצולעים משוכללים
בתוך מצולע המורכב מיותר משלוש צלעות ניתן להעביר אלכסון. האלכסון הוא קטע ישר בתוך המצולע המחבר שני קודקודים של המצולע שאינם מחוברים ביניהם על-ידי אחת מצלעותיו.

דוגמה אלכסון
[ עמוד ראשי - אלגברה והנדסה | הנדסת המישור : מבוא | מושגים בסיסיים | היסודות של הנדסת המישור | חיתוך שני ישרים | שני ישרים מקבילים | המצולע | המשולש | משפחת המרובעים | חישובי היקף ושטח | המעגל והעיגול | משולשים חופפים | יחס ופרופורציה של קטעים | משפט תאלס | יחס הזהב | דמיון משולשים | רשימת משפטים בהנדסה ]