משפחת המרובעים
המרובע הוא מצולע בעל ארבע צלעות.
למרובע יש ארבע צלעות, ארבעה קודקודים וארבע זוויות ומכאן שמו – מרובע.

דוגמה למרובעים
לפי הנוסחה לחישוב סכום הזוויות במצולע עולה כי סכום הזוויות במרובע הוא:
(4-2)•180º =
2•180º =
360º
נשים לב שבכל מרובע, ללא תלות בצורתו, סכום ארבעת הזוויות הפנימיות בו הוא תמיד 360º.
במרובע ניתן להעביר שני אלכסונים פנימיים.
גם את המרובע ניתן לסווג לסוגים שונים בהתאם למאפייני אורכי צלעותיו וגודל זוויותיו. לפי סיווג שני מאפיינים אלה נקבל את הגדרות המרובעים המיוחדים הבאים:
ריבוע הוא מרובע בו כל הצלעות שוות באורכיהן וכל הזוויות שוות בגודלן, משמע כולן זוויות ישרות.
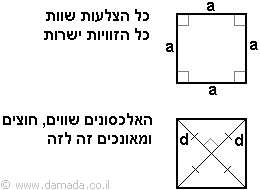
דוגמה לריבוע
בריבוע האלכסונים שווים באורכם ניצבים אחד לשני וחוצים זה את זה.
מלבן הוא מרובע בו כל צלע שווה באורכה לצלע שממולה, אך שונה מאורך הצלע הסמוכה לה, וכל הזוויות שוות בגודלן, משמע כולן זוויות ישרות.

דוגמה למלבן
במלבן האלכסונים שווים באורכם וחוצים זה את זה.
מקבילית היא מרובע בו כל צלע שווה באורכה לצלע שממולה, אך שונה מאורך הצלע הסמוכה לה, וכל זווית שווה בגודלה לזווית שממולה, אך שונה מגודל הזווית הסמוכה לה.
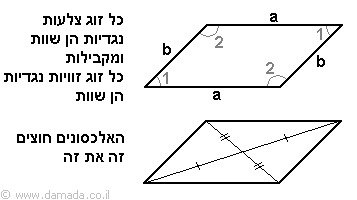
דוגמה למקבילית
במקבילית האלכסונים חוצים זה את זה.
מעוין הוא מרובע בו כל הצלעות שוות באורכיהן, וכל זווית שווה לזווית שממולה אך שונה מהזווית הסמוכה לה.

דוגמה למעוין
במעוין האלכסונים שווים באורכם וחוצים זה את זה.
טרפז הוא מרובע בו זוג אחד של צלעות הן מקבילות ולא שוות באורכיהן (הללו נקראות בסיסים), וזוג אחר של צלעות הן אינן מקבילות (הללו נקראות שוקיים).

דוגמה לטרפז
טרפז שווה-שוקיים הוא טרפז בו זוג צלעות השוקיים שוות באורכן. בטרפז שווה שוקיים האלכסונים שווים באורכם וחוצים זה את זה.
דלתון הוא מרובע בו זוג אחד של צלעות סמוכות הן שוות באורכיהן וזוג הצלעות האחר שוות גם הן באורכיהן אבל לגודל אחר. בין כל שתי הצלעות של כל אחד מהזוגות שלעיל מונחת זווית הנקראת זווית-ראש. זוג הזוויות שבין שני זוגות הצלעות נקראות זוויות הבסיס והן שוות בגודלן. בדלתון אין אף זוג צלעות נגדיות מקבילות.

דוגמה לדלתון
בדלתון האלכסונים ניצבים אחד לשני וגם האלכסון הראשי חוצה את האלכסון המשני.
[ עמוד ראשי - אלגברה והנדסה | הנדסת המישור : מבוא | מושגים בסיסיים | היסודות של הנדסת המישור | חיתוך שני ישרים | שני ישרים מקבילים | המצולע | המשולש | משפחת המרובעים | חישובי היקף ושטח | המעגל והעיגול | משולשים חופפים | יחס ופרופורציה של קטעים | משפט תאלס | יחס הזהב | דמיון משולשים | רשימת משפטים בהנדסה ]

[ עמוד הבית | אודות | זכויות יוצרים | מפת האתר ]

