חוק סנל

ווִילֵבְּרוֹרְד סְנֶל (Willebrord Snell)

נולד בשנת 1580 בהולנד, למשפחה אמידה. אביו היה חוקר ומתמטיקאי באוניברסיטה, לכן סנל הצעיר התוודע ללימודי המתמטיקה מוקדם יחסית. הוא גם החל ללמוד באוניברסיטה בגיל צעיר, תחילה בתחום משפטים אך חזר לתחום המתמטיקה, ואף עסק בהוראה כבר בהיותו בן 20 בלבד. בגיל 33 הוא החליף את אביו במשרת פרופסור באוניברסיטה. כארבע שנים לאחר מכן הוא הציג את עבודתו שעסקה בחישוב גדלי כדור-הארץ. עבודה זו, שהוא התחיל וגם סייע בסיומה הניחה את הבסיס למדע הגיאודזיה. שיטת המדידה בה סנל השתמש בעבודתו היא מדידת מרחקים בעזרת חלוקת השטח למשולשים גיאומטריים. שיטה זו אומצה כבסיס למדידות במדע הגיאודזיה.

סנל הציג עבודות נוספות במהלך חייו. בין היתר גם הצליח לחשב את ערכו של π 6 ספרות אחרי הנקודה העשרונית (עד לתקופתו היו ידועות רק שתי ספרות!).

...3.141592 = π

אך עבודתו העיקרית הייתה בתחום האופטיקה.

שני אנשים לפניו שחקרו את תחום האופטיקה ואת נושא שבירת קרני האור בפרט הם

תַּלְמֵי (Ptolemy)

שישב באלכסנדריה ואחריו

אַל-חָסֵן (Alhazen)

, איש מדע ממוצא ערבי. עבודתו של סנל הינה ייחודית בכך שהיא מקיפה ומפורטת וכוללת הסברים ונוסחאות לתופעת השבירה של גלים.

כאשר גל עובר מתווך אחד לתווך אחר ישנן שתי תופעות אפשריות. התופעה הראשונה היא החזרת חלק מהגל או כולו. הגל החוזר יימצא תמיד באותו מישור בו נמצא הגל הפוגע ובזווית נגדית זהה.

החזרה של גל

אם לא כל הגל חוזר תתרחש תופעה שנייה והיא שבירת הגל, כלומר המשך התקדמותו בתווך השני לא יהיה בהמשך קו ישר להתקדמותו בתווך הראשון, אלא בקו שבור.

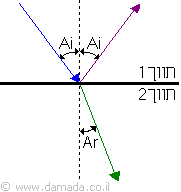
החזרה ושבירה של גל

תופעת השבירה של גלים מודגמת בפשטות כשחפץ כלשהו נמצא חציו בתוך מים וחציו מחוץ למים. במקרה כזה ייראה כאילו חציו שבתוך המים שבור ומוזז לעומת חציו שמחוץ למים.

בשנת 1611 גילה

יוֹהַאנְס קֶפְּלֵר (Johannes Kepler)

את תופעת ההחזרה הגמורה. החזרה גמורה מרחשת כאשר זווית הפגיעה Ai גדולה מספיק על מנת שזווית השבירה Ar הינה ˚90.

החזרה גמורה של גל

אך קפלר נכשל למצוא קשר מתמטי בין זווית השבירה לזווית הפגיעה. סנל, אגב, נפגש במהלך טיול שערך בין ערי אירופה בקפלר וב

טִיכוֹ בְּרַהַא (Tycho Brahe)

.

בשנת 1621 סנל מצא כי קיים קשר מתמטי בין זווית הפגיעה של גל בתווך לבין זווית השבירה שלו. סנל חישב ומצא כי הקשר מתקיים לפי הנוסחה הבאה:

sin Ai / sin Ar = n2 / n1
Ai היא זווית הפגיעה (Angle of Incidence)
Ar היא זווית השבירה (Angle of Refraction)
n1 הוא קבוע מקדם השבירה של תווך1
n2 הוא קבוע מקדם השבירה של תווך2

היחס n2 / n1 נקרא מקדם השבירה היחסי של תווך2 יחסית לתווך1. יחס זה מבטא את היחס ההפוך בין מהירות הגל בתוך שני התווכים לפי הנוסחה הבאה:

n2 / n1 = V1 / V2

להלן טבלת ערכים מספריים ליחס הנ"ל עבור אורך גל של 589 ננומטר העובר מתווך של ריק לתווכים נפוצים אחרים:

תווך	מקדם שבירה
ריק	1.0000
אוויר	1.0003
מים	1.333
שמן זית	1.460
זכוכית	1.5-1.9
יהלום	2.418
סיליקון	4.010

טבלת מקדמי שבירה של תווכים נפוצים

סנל נפטר ב-30 לאוקטובר 1626, בעיר הולדתו ליידן (Leiden) שבהולנד, והוא בן 46 בלבד. הוא לא פרסם את עבודתו בתחום האופטיקה. רק כשבעים שנה לאחר מותו התגלתה עבודתו על-ידי מתמטיקאי הולנדי אחר בשם

כְּרִיסְטִיאַן יוּגִינְס (Christiaan huygens)

, ממציא שעון המטוטלת, והעניקה לו את הכבוד הראוי.

דוגמה נוספת לשבירת גלי האור בתחום הנראה היא תופעת הקשת בשמיים. כאשר באזור אחד של השמיים אין עננים מתאפשרת חדירה של קרני השמש. אם באזור אחר מעונן וגשום אזי קרני השמש יישברו במעבר במסך הגשם. כל גל באורך שונה (כלומר גם בצבע נראה שונה) יישבר בזווית שונה ולכך תיווצר הפרדה של קרן האור למרכיביה – אורכי גל שונים בצבעים שונים. זוהי אותה תופעה הנצפית גם בשבירת קרן אור במנסרת פריזמה.

בשנת 1666 גילה

סֶר אַיְיזֵק נְיוּטוֹן (Sir Isaac Newton)

כי אור לבן נפרד למרכיביו, אורות בצבעים שונים, במעבר במנסרה.

ניסוי

חומרים
כלי זכוכית או פלסטיק שקוף בעל צורה מוארכת ובעל דפנות דקות יחסית לרוחבו
דף נייר וכלי כתיבה
סרגל
2 קיסמי עץ דקים (או גפרורים)

חלק ראשון – הוכחת הקשר בין זווית הפגיעה לזווית השבירה
1. הנח את כלי הזכוכית על אמצע דף הנייר ומלא אותו מים עד כדי חצי גובה של קיסם. סמן על הדף את מיקומו של הכלי.
2. העמד את הקיסם מאחורי כלי הזכוכית (לא בתוכו) כך שבמבט דרך כלי הזכוכית נראה חציו התחתון בתוך המים וחציו העליון מחוץ למים.
3. אם תביט בקו אנכי ישר לקיסם תראה את שני חצאיו ללא שבירה, אך אם תסיט את המבט הצידה תתחיל לראות שבירה של שני החצאים. השבירה גדלה ככל שזווית המבט גדלה.

ניסוי: מבט אנכי ישיר

ניסוי: מבט בזווית

4. מצא זווית מבט גדולה כך שעדיין ניתן לראות בבירור את שני חצאי הקיסם מבלי לחרוג ולהגיע לקצוות כלי הזכוכית שייתכן ומעוגלות. ייתכן ותצטרך למקמם את הקיסם במקום חדש מאחורי כלי הזכוכית לשם קבלת זווית שבירה מירבית. עשה זאת!
5. סמן על הנייר את מקום הקיסם שמאחורי כלי הזכוכית, זוהי הנקודה הראשונה.
6. החזק את הקיסם השני בידך וחזור והבט דרך כלי הזכוכית על הקיסם האחורי שנראה שבור. קל יהיה להתמקד בקיסם על-ידי עצימת עין אחת.
7. כעת השתמש בקיסם השני ומקם אותו לפי כלי הזכוכית כך שיתלכד עם החלק העליון של הקיסם האחורי. סמן נקודה זו, נקודה שניה, על הדף.
8. חזור שוב לאותה זווית מבט. וודא שהינך באותה זווית מבט על ידי מיקום הקיסם הקדמי באותה נקודה המסומנת כבר על הדף וודא שהוא מלכד עם החצי העליון של הקיסם האחורי. כעת הזז את הקיסם הקדמי כך שהפעם יתלכד עם החצי התחתון של הקיסם האחורי (זה שנראה כבתוך המים). סמן את הנקודה הזו, השלישית, על הדף.
9. חזור שוב לאותה זווית מבט. הפעם מקם גם את הקיסם השני מאחורי כלי הזכוכית כך שחציו העליון יתלכד עם החצי התחתון של הקיסם הראשון. סמן את הנקודה הרביעית על הדף.

סמן על הדף את הקווים הבאים בין ארבעת הנקודות שסימנת. כדלקמן:

ניסוי: חישוב מקדם השבירה של מים

נזכיר שסינוס זווית שווה לניצב שמול הזווית חלקי היתר, כלומר B/C עבור זווית הפגיעה ו- b/c עבור זווית השבירה.

כבר ידוע לנו שגל האור נשבר במעבר בתוך תווך כך שזווית יציאתו מהתווך זהה לזווית כניסתו לתווך רק מוזזת. המשמעות היא שמסלול יציאתו של הגל מהתווך היא בקו מקביל למסלול כניסתו לתווך. תוכל לבדוק את נכונות 4 הנקודות שסימנת בעזרת בדיקה אם שני הקווים מקבילים (פחות או יותר). אם שני הקווים אינם מקבילים בקירוב, אז תצטרך לחזור שוב על המדידות בדיוק רב יותר או לבחור כלי זכוכית אחר יותר מתאים מבחינת מידותיו.

חשב את מקדם השבירה של המים בעזרת הנוסחה

n1 sin A1 = n2 sin A2

ניתן להזניח את n1 שהוא מקדם השבירה של אוויר ולהציב 1 במקומו.
אני קיבלתי את התוצאה הבאה:

1 * (3/5.1) = n2 (5.1/11.1)

n2 = 1.28

שים לב, מכיוון שדפנות כלי הזכוכית דקות מאוד יחסית לרוחבו אזי ניתן להזניח בקירוב טוב את השפעתן על שבירת הגל ולהניח שמקור כל השבירה הינו במים.

כידוע מקדם השבירה של מים הנו 1.333, כלומר התוצאה שקיבלתי היא באחוז דיוק של,

(1.333-1.28)/1.333 = 3.98%

וזו תוצאה סבירה לניסוי ביתי.

אגב, תוכל לחזור על הניסוי עבור תווך אחר למשל שמן-זית. ישנם בקבוקי שמן-זית עשויים זכוכית בעלי צורה מלבנית מוארכת שמתאימים לעריכת הניסוי. אני קיבלתי שמקדם השבירה של שמן-זית הוא 1.39. זו תוצאה בדיוק של

(1.46-1.39)/1.46 = 4.8%.

חלק שני – הוכחת הקשר בין זווית הפגיעה לזווית השבירה
מבחינה הגיונית חלק זה אמור להיות לפני החלק הראשון. אך מכיוון שחלק זה ארוך יותר (בעצם כולל פעמיים את מהלך החלק הראשון) הפכתי אותו לחלק שני.

חזור שוב על החלק הראשון, הפעם נסה למצוא זווית מבט שתהא חצי בקירוב לזווית השבירה של חלק ראשון. כלומר, מצא הבט דרך כלי הזכוכית על הקיסם האחורי בזווית קטנה יותר. סמן שלושה נקודות חדשות על הדף והעבר את הקווים בהתאם.

הוכח כי היחס n1/n2 מתקיים וזהה בין שתי המדידות שערכת. כלומר הוכח כי Sin A2 / Sin A1 מהחלק הראשון של הניסוי שווה ל Sin A2 / Sin A1 שקיבלת מהמדידות החדשות.

לשנים: 1990-2000

■...■...■...■...■ | שלום | ■...■...■...■...■